Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Array and Array Operations”.
1. Which of these best describes an array?
a) A data structure that shows a hierarchical behavior
b) Container of objects of similar types
c) Arrays are immutable once initialised
d) Array is not a data structure
Explanation: Array contains elements only of the same type.
2. How do you initialize an array in C?
a) int arr[3] = (1,2,3);
b) int arr(3) = {1,2,3};
c) int arr[3] = {1,2,3};
d) int arr(3) = (1,2,3);
Explanation: This is the syntax to initialize an array in C.
3. How do you instantiate an array in Java?
a) int arr[] = new int(3);
b) int arr[];
c) int arr[] = new int[3];
d) int arr() = new int(3);
Explanation: Note that int arr[]; is declaration whereas int arr[] = new int[3]; is to instantiate an array.
4. Which of the following is the correct way to declare a multidimensional array in Java?
a) int[] arr;
b) int arr[[]];
c) int[][]arr;
d) int[[]] arr;
Explanation: The syntax to declare multidimensional array in java is either int[][] arr; or int arr[][];
5. What is the output of the following Java code?
array main args arr ,,,, ..arr ..arr
a) 3 and 5
b) 5 and 3
c) 2 and 4
d) 4 and 2
Explanation: Array indexing starts from 0.
6. What is the output of the following Java code?
array main args arr ,,,, ..arr
a) 4
b) 5
c) ArrayIndexOutOfBoundsException
d) InavlidInputException
Explanation: Trying to access an element beyond the limits of an array gives ArrayIndexOutOfBoundsException.
7. When does the ArrayIndexOutOfBoundsException occur?
a) Compile-time
b) Run-time
c) Not an error
d) Not an exception at all
Explanation: ArrayIndexOutOfBoundsException is a run-time exception and the compilation is error-free.
8. Which of the following concepts make extensive use of arrays?
a) Binary trees
b) Scheduling of processes
c) Caching
d) Spatial locality
Explanation: Whenever a particular memory location is referred to, it is likely that the locations nearby are also referred, arrays are stored as contiguous blocks in memory, so if you want to access array elements, spatial locality makes it to access quickly.
9. What are the advantages of arrays?
a) Objects of mixed data types can be stored
b) Elements in an array cannot be sorted
c) Index of first element of an array is 1
d) Easier to store elements of same data type
Explanation: Arrays store elements of the same data type and present in continuous memory locations.
Explanation: Arrays are of fixed size. If we insert elements less than the allocated size, unoccupied positions can’t be used again. Wastage will occur in memory.
11. Assuming int is of 4bytes, what is the size of int arr[15];?
a) 15
b) 19
c) 11
d) 60
Explanation: Since there are 15 int elements and each int is of 4bytes, we get 15*4 = 60bytes.
12. In general, the index of the first element in an array is __________
a) 0
b) -1
c) 2
d) 1
Explanation: In general, Array Indexing starts from 0. Thus, the index of the first element in an array is 0.
13. Elements in an array are accessed _____________
a) randomly
b) sequentially
c) exponentially
d) logarithmically
Explanation: Elements in an array are accessed randomly. In Linked lists, elements are accessed sequentially.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Circular Linked List”.
1. What differentiates a circular linked list from a normal linked list?
a) You cannot have the ‘next’ pointer point to null in a circular linked list
b) It is faster to traverse the circular linked list
c) You may or may not have the ‘next’ pointer point to null in a circular linked list
d) Head node is known in circular linked list
Explanation: The ‘next’ pointer points to null only when the list is empty, otherwise it points to the head of the list. Every node in a circular linked list can be a starting point(head).
2. How do you count the number of elements in the circular linked list?
a)
lengthNode head length head Node temp head. temp head temp temp. length length
b)
lengthNode head length head Node temp head. temp temp temp. length length
c)
lengthNode head length head Node temp head. temp head temp temp head. length length
d)
lengthNode head length head Node temp head. temp head temp temp head. length length
Explanation: If the head is null, it means that the list is empty. Otherwise, traverse the list until the head of the list is reached.
3. What is the functionality of the following piece of code? Select the most appropriate.
function data flag head Node temp head. temp head temp. data temp temp. flag flag .. ..
a) Print success if a particular element is not found
b) Print fail if a particular element is not found
c) Print success if a particular element is equal to 1
d) Print fail if the list is empty
Explanation: The function prints fail if the given element is not found. Note that this option is inclusive of option “Print fail if the list is empty”, the list being empty is one of the cases covered.
4. What is the time complexity of searching for an element in a circular linked list?
a) O(n)
b) O(nlogn)
c) O(1)
d) O(n2)
Explanation: In the worst case, you have to traverse through the entire list of n elements.
5. Which of the following application makes use of a circular linked list?
a) Undo operation in a text editor
b) Recursive function calls
c) Allocating CPU to resources
d) Implement Hash Tables
Explanation: Generally, round robin fashion is employed to allocate CPU time to resources which makes use of the circular linked list data structure. Recursive function calls use stack data structure. Undo Operation in text editor uses doubly linked lists. Hash tables uses singly linked lists.
insertHead data Node temp Nodedata Node cur head cur. head cur cur. head head temp head.head temp.head head temp cur.temp size
b)
insertHead data Node temp Nodedata cur head cur cur. head head temp head.head temp.head. cur.temp size
c)
insertHead data Node temp Nodedata head head temp head.head temp.head. head temp size
d)
insertHead data Node temp Nodedata head head temp head.head. temp.head. head temp size
Explanation: If the list is empty make the new node as ‘head’, otherwise traverse the list to the end and make its ‘next’ pointer point to the new node, set the new node’s next point to the current head and make the new node as the head.
7. What is the functionality of the following code? Choose the most appropriate answer.
function head . var Node temp head temp. head temp temp. temp head var head. head var temp.head. var head. head head. var
a) Return data from the end of the list
b) Returns the data and deletes the node at the end of the list
c) Returns the data from the beginning of the list
d) Returns the data and deletes the node from the beginning of the list
Explanation: First traverse through the list to find the end node, then manipulate the ‘next’ pointer such that it points to the current head’s next node, return the data stored in head and make this next node as the head.
8. What is the functionality of the following code? Choose the most appropriate answer.
function head . var Node temp head Node cur temp. head cur temp temp temp. temp head var head. head var var temp. cur.head var
a) Return data from the end of the list
b) Returns the data and deletes the node at the end of the list
c) Returns the data from the beginning of the list
d) Returns the data and deletes the node from the beginning of the list
Explanation: First traverse through the list to find the end node, also have a trailing pointer to find the penultimate node, make this trailing pointer’s ‘next’ point to the head and return the data stored in the ‘temp’ node.
9. Which of the following is false about a circular linked list?
a) Every node has a successor
b) Time complexity of inserting a new node at the head of the list is O(1)
c) Time complexity for deleting the last node is O(n)
d) We can traverse the whole circular linked list by starting from any point
Explanation: Time complexity of inserting a new node at the head of the list is O(n) because you have to traverse through the list to find the tail node.
10. Consider a small circular linked list. How to detect the presence of cycles in this list effectively?
a) Keep one node as head and traverse another temp node till the end to check if its ‘next points to head
b) Have fast and slow pointers with the fast pointer advancing two nodes
at a time and slow pointer advancing by one node at a time
c) Cannot determine, you have to pre-define if the list contains cycles
d) Circular linked list itself represents a cycle. So no new cycles cannot be generated
Explanation: Advance the pointers in such a way that the fast pointer advances two nodes at a time and slow pointer advances one node at a time and check to see if at any given instant of time if the fast pointer points to slow pointer or if the fast pointer’s ‘next’ points to the slow pointer. This is applicable for smaller lists.
This set of Data Structure Interview Questions and Answers for Experienced people focuses on “Decimal to Binary using Stacks”.
1. Express -15 as a 6-bit signed binary number.
a) 001111
b) 101111
c) 101110
d) 001110
Explanation: The first 4 1s from the right represent the number 15, 2 more bits are padded to make it 6 digits and the leftmost bit is a 1 to represent that it is -15.
2. Which of the following code snippet is used to convert decimal to binary numbers?
a)
convertBinary num
bin
index
num
binindex num2
num num
i indexi i
..bini
b)
convertBinary num
bin
index
num
binindex num2
num num
i indexi i
..bini
c)
convertBinary num
bin
index
num
binindex num
num num2
i indexi i
..bini
d)
convertBinary num
bin
index
num
binindex num
num num2
i indexi i
..bini
Explanation: Take the modulus by 2 of the number and store in an array while halving the number during each iteration and then display the contents of the array.
3. Which is the predefined method available in Java to convert decimal to binary numbers?
a) toBinaryInteger(int)
b) toBinaryValue(int)
c) toBinaryNumber(int)
d) toBinaryString(int)
Explanation: The method toBinaryString() takes an integer argument and is defined in java.lang package. Usage is java.lang.Integer.toBinaryString(int) this returns the string representation of the unsigned integer value.
4. Using stacks, how to obtain the binary representation of the number?
a)
convertBinary num
StackInteger stack StackInteger
num
digit num
stack.digit
num num
..
stack.
..stack.
convertBinary num
StackInteger stack StackInteger
num
digit num
stack.digit
..
stack.
..stack.
c)
convertBinary num
StackInteger stack StackInteger
num
digit num
stack.digit
num num
..
stack.
..stack.
d)
convertBinary num
StackInteger stack StackInteger
num
digit num
stack.digit2
num num
..
stack.
..stack.
Explanation: Here instead of adding the digits to an array, you push it into a stack and while printing, pop it from the stack.
5. What is the time complexity for converting decimal to binary numbers?
a) O(1)
b) O(n)
c) O(logn)
d) O(nlogn)
Explanation: Since each time you are halving the number, it can be related to that of a binary search algorithm, hence the complexity is O(logn).
6. Write a piece of code which returns true if the string contains balanced parenthesis, false otherwise.
a)
isBalanced exp
len exp.
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
stk.
stk.
b)
isBalanced exp
len exp.
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
stk.
stk.
c)
isBalanced exp
len exp.
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
stk.
stk.
d)
isBalanced exp
len exp.
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
stk.
stk.
Explanation: Whenever a ‘(‘ is encountered, push it into the stack, and when a ‘)’ is encountered check the top of the stack to see if there is a matching ‘(‘, if not return false, continue this till the entire string is processed and then return true.
7. What is the time complexity of the following code?
isBalanced exp
len exp.
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
stk.
stk.
a) O(logn)
b) O(n)
c) O(1)
d) O(nlogn)
Explanation: All the characters in the string have to be processed, hence the complexity is O(n).
8. Which of the following program prints the index of every matching parenthesis?
a)
dispIndex exp
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
p stk.
..ip
e
..i
stk.
..stk.
b)
dispIndex exp
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
p stk.
..ip
e
..i
stk.
..stk.
c)
dispIndex exp
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
p stk.
..ip
e
..i
stk.
..stk.
d)
dispIndex exp
StackInteger stk StackInteger
i i len i
ch exp.i
ch
stk.i
ch
p stk.
..ip
e
..i
stk.
..stk.
Explanation: Whenever a ‘(‘ is encountered, push the index of that character into the stack, so that whenever a corresponding ‘)’ is encountered, you can pop and print it.
Participate in the Sanfoundry Certification contest to get free Certificate of Merit. Join our social networks below and stay updated with latest contests, videos, internships and jobs!
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Prefix to Infix Conversion”.
1. What would be the solution to the given prefix notation?
a) 2
b) 5
c) 10
d) 7
Explanation: The infix notation of the given prefix notation is 5+10/5-5 which gives us 2 as our answer.
2. What would be the solution to the given prefix notation?
a) 1
b) 4
c) 2
d) 8
Explanation: The infix notation to the given prefix notation is 16/4/2/1 which gives us 1 as our answer. The infix notation is got from the prefix notation by traversing the equation from the right.
3. What would be the solution to the given prefix notation?
a) 14
b) 15
c) 18
d) 12
Explanation: The infix notation for the given prefix notation is (9+(3*(8/4))) which solves to 15. So 15 is correct answer.
4. What would be the solution to the given prefix notation?
a) 6
b) -6
c) 3
d) -3
Explanation: The infix notation for the given prefix notation is (1+2)-3*(6/2). The result of the given equation is -6.
5. What would be the solution to the given prefix notation?
a) 1
b) 0
c) -1
d) -2
Explanation: The infix notation for the given prefix notation is (1*5)-(6/3)*6/2. The result of the equation is -1.
a) 12
b) 7.5
c) 9
d) 13.5
Explanation: The infix notation of the given prefix notation is ((1+2)/(4/2))*(3+5) which solves to (3/2)*8 which by solving gives us 12.
7. Given a prefix and a postfix notation what are the difference between them?
a) The postfix equation is solved starting from the left whereas the prefix notation is solved from the right
b) The postfix equation is solved starting from the right whereas the prefix notation is solved from the left
c) Both equations are solved starting from the same side(right)
d) Both equations are solved starting from the same side(left)
Explanation: The postfix notation is solved starting from left but whereas the prefix notation is reversed after creating them, therefore it’s solved starting from right.
8. When converting the prefix notation into an infix notation, the first step to be followed is ________
a) Reverse the equation
b) Push the equation to the stack
c) Push the equation onto the queue
d) Push the equation to the stack or queue
Explanation: The steps that are followed are: the equation is reversed, pushed onto a stack, popped one by one and solved. Therefore the first step is reversing the equation.
9. The time complexity of converting a prefix notation to infix notation is _________
a) O(n) where n is the length of the equation
b) O(n) where n is number of operands
c) O(1)
d) O(logn) where n is length of the equation
Explanation: The processes that are involved are reversing the equation (O(n)), pushing them all onto the stack(O(n)), and popping them one by one and solving them (O(n)). Hence the answer is O(n) where n is the length of the equation.
10. Given two processes (conversion of postfix equation to infix
notation and conversion of prefix notation to infix notation), which of
the following is easier to implement?
a) Both are easy to implement
b) Conversion of postfix equation to infix equation is harder than converting a prefix notation to infix notation
c) Conversion of postfix equation to infix equation is easier than converting a prefix notation to infix notation
d) Insufficient data
Explanation: As the conversion of prefix notation to infix notation involves reversing the equation, the latter is harder to implement than postfix to infix process.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Bit Array”.
1. What is a bit array?
a) Data structure for representing arrays of records
b) Data structure that compactly stores bits
c) An array in which most of the elements have the same value
d) Array in which elements are not present in continuous locations
Explanation: It compactly stores bits and exploits bit-level parallelism.
2. Which of the following bitwise operations will you use to set a particular bit to 1?
a) OR
b) AND
c) XOR
d) NOR
Explanation: 1 OR 1 = 1, 0 OR 1 = 1, any bit OR’ed with 1 gives 1.
3. Which of the following bitwise operations will you use to set a particular bit to 0?
a) OR
b) AND
c) XOR
d) NAND
Explanation: 1 AND 0 = 0, 0 AND 0 = 0, any bit AND with 0 gives 0.
4. Which of the following bitwise operations will you use to toggle a particular bit?
a) OR
b) AND
c) XOR
d) NOT
Explanation: 1 XOR 1 = 0, 0 XOR 1 = 1, note that NOT inverts all the bits, while XOR toggles only a specified bit.
5. Which of the following is not an advantage of bit array?
a) Exploit bit level parallelism
b) Maximal use of data cache
c) Can be stored and manipulated in the register set for long periods of time
d) Accessing Individual Elements is easy
Explanation: Individual Elements are difficult to access and can’t be accessed in some programming languages. If random access is more common than sequential access, they have to be compressed to byte/word array. Exploit Bit parallelism, Maximal use of data cache and storage and manipulation for longer time in register set are all advantages of bit array.
6. Which of the following is not a disadvantage of bit array?
a) Without compression, they might become sparse
b) Accessing individual bits is expensive
c) Compressing bit array to byte/word array, the machine also has to support byte/word addressing
d) Storing and Manipulating in the register set for long periods of time
Explanation: Bit arrays allow small arrays of bits to be stored and manipulated in the register set for long periods of time with no memory accesses because of their ability to exploit bit-level parallelism, limit memory access, and maximally use the data cache, they often outperform many other data structures on practical data sets. This is an advantage of bit array. The rest are all disadvantages of bit array.
7. Which of the following is/are not applications of bit arrays?
a) Used by the Linux kernel
b) For the allocation of memory pages
c) Bloom filter
d) Implementation of Vectors and Matrices
Explanation: Normal Arrays are used to implement vectors and matrices. Bit arrays have no prominent role. Remaining all are applications of Bit Arrays.
8. Which class in Java can be used to represent bit array?
a) BitSet
b) BitVector
c) BitArray
d) BitStream
Explanation: The BitSet class creates a special type of array that can hold bit values.
9. Which of the following bitwise operator will you use to invert all the bits in a bit array?
a) OR
b) NOT
c) XOR
d) NAND
Explanation: NOT operation is used to invert all the bits stored in a bit array.
Eg: NOT (10110010) = 01001101.
10. Run-Length encoding is used to compress data in bit arrays.
a) True
b) False
Explanation: A bit array stores the combinations of bit 0 and bit 1. Each bit in the bit array is independent. Run Length encoding is a data compression technique in which data are stored as single value and number of times that value repeated in the data. This compression reduces the space complexity in arrays. Bit arrays without compression require more space. Thus, we will use Run-Length encoding in most of the cases to compress data in bit arrays.
11. What does Hamming weight/population count mean in Bit arrays?
a) Finding the number of 1 bit in a bit array
b) Finding the number of 0 bit in a bit array
c) Finding the sum of bits in a bit array
d) Finding the average number of 1’s and 0’s in bit arrays
Explanation: Hamming/ population count involves finding the number of 1’s in the bit array. Population count is used in data compression.
Explanation: Bit field contains the number of adjacent computer locations used to store the sequence of bits to address a bit or groups of bits. Bit array is an array that stores combinations of bit 0 and bit 1. Thus, bit fields and Bit arrays are different.
13. Which one of the following operations returns the first occurrence of bit 1 in bit arrays?
a) Find First Zero
b) Find First One
c) Counting lead Zeroes
d) Counting lead One
Explanation: Find First One operation returns the first occurrence of bit 1 in the bit array. Find First Zero operation returns the first occurrence of bit 0 in the bit array. If the most significant bit in bit array is 1, then count lead zeroes operation returns the number of zeroes present before the most significant bit. If the most significant bit in bit array is 0, then the count lead one returns the number of ones present before the most significant bit.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Sparse Matrix”.
1. Which matrix has most of the elements (not all) as Zero?
a) Identity Matrix
b) Unit Matrix
c) Sparse Matrix
d) Zero Matrix
Explanation: Sparse Matrix is a matrix in which most of the elements are Zero. Identity Matrix is a matrix in which all principle diagonal elements are 1 and rest of the elements are Zero. Unit Matrix is also called Identity Matrix. Zero Matrix is a matrix in which all the elements are Zero.
2. What is the relation between Sparsity and Density of a matrix?
a) Sparsity = 1 – Density
b) Sparsity = 1 + Density
c) Sparsity = Density*Total number of elements
d) Sparsity = Density/Total number of elements
Explanation: Sparsity of a matrix is equal to 1 minus Density of the matrix. The Sparsity of matrix is defined as the total number of Zero Valued elements divided total number of elements.
3. Who coined the term Sparse Matrix?
a) Harry Markowitz
b) James Sylvester
c) Chris Messina
d) Arthur Cayley
Explanation: Harry Markowitz coined the term Sparse Matrix. James Sylvester coined the term Matrix. Chris Messina coined the term Hashtag and Arthur Cayley developed the algebraic aspects of a matrix.
4. Is O(n) the Worst case Time Complexity for addition of two Sparse Matrix?
a) True
b) False
Explanation: In Addition, the matrix is traversed linearly, hence it has the time complexity of O(n) where n is the number of non-zero elements in the largest matrix amongst two.
5. The matrix contains m rows and n columns. The matrix is called Sparse Matrix if ________
a) Total number of Zero elements > (m*n)/2
b) Total number of Zero elements = m + n
c) Total number of Zero elements = m/n
d) Total number of Zero elements = m-n
Explanation: For matrix to be Sparse Matrix, it should contain Zero elements more than the non-zero elements. Total elements of the given matrix is m*n. So if Total number of Zero elements > (m*n)/2, then the matrix is called Sparse Matrix.
6. Which of the following is not the method to represent Sparse Matrix?
a) Dictionary of Keys
b) Linked List
c) Array
d) Heap
Explanation: Heap is not used to represent Sparse Matrix while in Dictionary, rows and column numbers are used as Keys and values as Matrix entries, Linked List is used with each node of Four fields (Row, Column, Value, Next Node) (2D array is used to represent the Sparse Matrix with three fields (Row, Column, Value).
7. Is Sparse Matrix also known as Dense Matrix?
a) True
b) False
Explanation: Sparse Matrix is a matrix with most of the elements as Zero elements while Dense Matrix is a matrix with most of the elements as Non-Zero element.
8. Which one of the following is a Special Sparse Matrix?
a) Band Matrix
b) Skew Matrix
c) Null matrix
d) Unit matrix
Explanation: A band matrix is a sparse matrix whose non zero elements are bounded to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.
9. In what way the Symmetry Sparse Matrix can be stored efficiently?
a) Heap
b) Binary tree
c) Hash table
d) Adjacency List
Explanation: Since Symmetry Sparse Matrix arises as the adjacency matrix of the undirected graph. Hence it can be stored efficiently as an adjacency list.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Skip List”.
1. What is a skip list?
a) a linkedlist with size value in nodes
b) a linkedlist that allows faster search within an ordered sequence
c) a linkedlist that allows slower search within an ordered sequence
d) a tree which is in the form of linked list
Explanation: It is a datastructure, which can make search in sorted linked list faster in the same way as binary search tree and sorted array (using binary search) are faster.
2. Consider the 2-level skip list
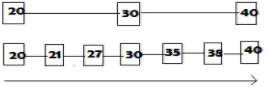
How to access 38?
a) travel 20-30-35-38
b) travel 20-30-40-38
c) travel 20-38
d) travel 20-40-38
Explanation: Let us call the nodes 20, 30, 40 as top lines and the nodes between them as normal lines. the advantage of skip lists is we can skip all the elements between the top line elements as required.
3. Skip lists are similar to which of the following datastructure?
a) stack
b) heap
c) binary search tree
d) balanced binary search tree
Explanation: Skip lists have the same asymptotic time complexity as balanced binary search tree. For a Balanced Binary Search Tree, we skip almost half of the nodes after one comparison with root element. The same thing done in the skip lists. Hence skip lists are similar to balanced Binary search trees.
4. What is the time complexity improvement of skip lists from linked lists in insertion and deletion?
a) O(n) to O(logn) where n is number of elements
b) O(n) to O(1) where n is number of elements
c) no change
d) O(n) to O(n2) where n is number of elements
Explanation: In Skip list we skip some of the elements by adding more layers. In this the skip list resembles balanced binary search trees. Thus we can change the time complexity from O (n) to O (logn)
5. To which datastructure are skip lists similar to in terms of time complexities in worst and best cases?
a) balanced binary search trees
b) binary search trees
c) binary trees
d) linked lists
Explanation: Skip lists are similar to any randomly built binary search tree. a BST is balanced because to avoid skew tree formations in case of sequential input and hence achieve O(logn) in all 3 cases. now skip lists can gurantee that O(logn) complexity for any input.
6. The nodes in a skip list may have many forward references. their number is determined
a) probabilistically
b) randomly
c) sequentially
d) orthogonally
Explanation: The number of forward references are determined probabilistically, that is why skip list is a probabilistic algorithm.
7. Are the below statements true about skiplists?
In a sorted set of elements skip lists can implement the below operations
i.given a element find closest element to the given value in the sorted set in O(logn)
ii.find the number of elements in the set whose values fall a given range in O(logn)
a) true
b) false
Explanation: To achieve above operations augment with few additional stuff like partial counts.
8. How to maintain multi-level skip list properties when insertions and deletions are done?
a) design each level of a multi-level skip list with varied probabilities
b) that cannot be maintained
c) rebalancing of lists
d) reconstruction
Explanation: For example consider a 2 level skip list. the level-2 skip list can skip one node on a average and at some places may skip 2 nodes, depending on probabilities. this ensures O(logn).
9. Is a skip list like balanced tree?
a) true
b) false
Explanation: Skip list behaves as a balanced tree with high probability and can be commented as such because nodes with different heights are mixed up evenly.
10. What is indexed skip list?
a) it stores width of link in place of element
b) it stores index values
c) array based linked list
d) indexed tree
Explanation: The width is defined as number of bottom layer links that are being traversed by each of higher layer elements. e.g: for a level-2 skip lists, all level-1 nodes have 1 as width, for level-2 width will be 2.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Xor Linked List”.
1. What is xor linked list ?
a) uses of bitwise XOR operation to decrease storage requirements for doubly linked lists
b) uses of bitwise XOR operation to decrease storage requirements for linked lists
c) uses of bitwise operations to decrease storage requirements for doubly linked lists
d) just another form of linked list
Explanation: Why we use bitwise XOR operation is to decrease storage requirements for doubly linked lists.
2. What does a xor linked list have ?
a) every node stores the XOR of addresses of previous and next nodes
b) actuall memory address of next node
c) every node stores the XOR of addresses of previous and next two nodes
d) every node stores xor 0 and the current node address
Explanation: Every node stores the XOR of addresses.
3. What does first and last nodes of a xor linked lists contain ? (let address of first and last be A and B)
a) NULL xor A and B xor NULL
b) NULL and NULL
c) A and B
d) NULL xor A and B
Explanation: NULL xor A and B xor NULL.
4. Which of the following is an advantage of XOR list?
a) Almost of debugging tools cannot follow the XOR chain, making debugging difficult
b) You need to remember the address of the previously accessed node in order to calculate the next node’s address
c) In some contexts XOR of pointers is not defined
d) XOR list decreases the space requirement in doubly linked list
Explanation: XOR linked list stores the address of previous and next nodes by performing XOR operations. It requires single pointer to store both XOR address of next and previous nodes. Thus it reduces space. It is an advantage. But the main disadvantages are debugging tools cannot follow XOR chain, previous node address must be remembered to get next nodes and pointers are not defined accurately.
5. Which of the following is not the properties of XOR lists?
a) X⊕X = 0
b) X⊕0 = X
c) (X⊕Y)⊕Z = X⊕(Y⊕Z)
d) X⊕0 = 1
Explanation: The important properties of XOR lists are X⊕X=0 , X⊕0=X and (X⊕Y)⊕Z = X⊕(Y⊕Z).
6. Which of the following statements are true ?
i) practical application of XOR linked lists are in environments with limited space requirements, such as embedded devices.
ii)xor lists are not suitable because most garbage collectors will fail
to work properly with classes or structures that don’t contain literal
pointers
iii)in order to calculate the address of the next node you need to remember the address of the previous node
iv)xor lists are much efficient than single, doubly linked lists and arrays
a) i, ii, iii, iv
b) i, ii, iii
c) i, ii
d) i
Explanation: Xor lists requires same time for most of the operations as arrays would require.
7. What’s wrong with this code which returns xor of two nodes address ?
struct node XOR struct node a, struct node b
a b
a) nothing wrong. everything is fine
b) type casting at return is missing
c) parameters are wrong
d) total logic is wrong
Explanation: It must be typecasted– return (struct node*)((int) (a) (int) (b));
8. Given 10,8,6,7,9
swap the above numbers such that finally you got 6,7,8,9,10
so now reverse 10
9,7,6,8,10
now reverse 9
8,6,7,9,10
7,6,8,9,10
6,7,8,9,10
at this point 6 is ahead so no more reversing can be done so stop.
To implement above algorithm which datastructure is better and why ?
a) linked list. because we can swap elements easily
b) arrays. because we can swap elements easily
c) xor linked list. because there is no overhead of pointers and so memory is saved
d) doubly linked list. because you can traverse back and forth
Explanation: XOR linked lists are used to reduce the memory by storing the XOR values of address instead of actual address in pointers.
9. Consider the following pseudocode of insertion in XOR list and write the approximate code snippet of it.
xorlinkedlist insertstruct node head_ref, value
node new_node struct node
new_nodevalue value
new_nodenodepointerxored xor head_ref,
head_pointer
printf
let b,c,d are nodes and a is to be inserted at beginning, a address field must contain xor b and b
address filed must be a xor c.
head_pointer new_node
a)
node next XOR head_refnpx, head_refnpx XOR new_node, next
node next XOR head_refnpx, head_ref XOR new_node, next
c)
node next XOR head_refnpx, head_refnpxnpx XOR new_node, next
d)
node next XOR head_ref, head_refnpx XOR new_node, next
Explanation: They code for the english is
node next XOR head_refnpx, head_refnpx XOR new_node, next
.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Binary Trees using Array”.
1. How many children does a binary tree have?
a) 2
b) any number of children
c) 0 or 1 or 2
d) 0 or 1
Explanation: Can have atmost 2 nodes.
2. What is/are the disadvantages of implementing tree using normal arrays?
a) difficulty in knowing children nodes of a node
b) difficult in finding the parent of a node
c) have to know the maximum number of nodes possible before creation of trees
d) difficult to implement
Explanation: The size of array is fixed in normal arrays. We need to know the number of nodes in the tree before array declaration. It is the main disadvantage of using arrays to represent binary trees.
3. What must be the ideal size of array if the height of tree is ‘l’?
a) 2l-1
b) l-1
c) l
d) 2l
Explanation: Maximum elements in a tree (complete binary tree in worst case) of height ‘L’ is 2L-1. Hence size of array is taken as 2L-1.
4. What are the children for node ‘w’ of a complete-binary tree in an array representation?
a) 2w and 2w+1
b) 2+w and 2-w
c) w+1/2 and w/2
d) w-1/2 and w+1/2
Explanation: The left child is generally taken as 2*w whereas the right child will be taken as 2*w+1 because root node is present at index 0 in the array and to access every index position in the array.
5. What is the parent for a node ‘w’ of a complete binary tree in an array representation when w is not 0?
a) floor(w-1/2)
b) ceil(w-1/2)
c) w-1/2
d) w/2
Explanation: Floor of w-1/2 because we can’t miss a node.
6. If the tree is not a complete binary tree then what changes can be made for easy access of children of a node in the array?
a) every node stores data saying which of its children exist in the array
b) no need of any changes continue with 2w and 2w+1, if node is at i
c) keep a seperate table telling children of a node
d) use another array parallel to the array with tree
Explanation: Array cannot represent arbitrary shaped trees. It can only be used in case of complete trees. If every node stores data saying that which of its children exists in the array then elements can be accessed easily.
7. What must be the missing logic in place of missing lines for finding sum of nodes of binary tree in alternate levels?
npower,height
iin
jjpow,currentlevelj
sumsumai
ii
a)
iipow,currentlevel currentlevelcurrentlevel j
b)
iipow,currentlevel currentlevelcurrentlevel j
c)
iipow,currentlevel currentlevelcurrentlevel j
d)
iipow,currentlevel currentlevelcurrentlevel j
Explanation: The i value must skip through all nodes in the next level and current level must be one+next level.
8. Consider a situation of writing a binary tree into a file with
memory storage efficiency in mind, is array representation of tree is
good?
a) yes because we are overcoming the need of pointers and so space efficiency
b) yes because array values are indexable
c) No it is not efficient in case of sparse trees and remaning cases it is fine
d) No linked list representation of tree is only fine
Explanation: In case of sparse trees (where one node per level in worst cases), the array size (2h)-1 where h is height but only h indexes will be filled and (2h)-1-h nodes will be left unused leading to space wastage.
9. Why is heap implemented using array representations than tree(linked list) representations though both tree representations and heaps have same complexities?
binary heap insert Olog n delete min Olog n a tree insert Olog n delete Olog n
Then why go with array representation when both are having same values ?
a) arrays can store trees which are complete and heaps are not complete
b) lists representation takes more memory hence memory efficiency is less and go with arrays and arrays have better caching
c) lists have better caching
d) In lists insertion and deletion is difficult
Explanation: In memory the pointer address for next node may not be adjacent or nearer to each other and also array have wonderful caching power from os and manipulating pointers is a overhead. Heap data structure is always a complete binary tree.
10. Can a tree stored in an array using either one of inorder or post order or pre order traversals be again reformed?
a) Yes just traverse through the array and form the tree
b) No we need one more traversal to form a tree
c) No in case of sparse trees
d) Yes by using both inorder and array elements
Explanation: We need any two traversals for tree formation but if some additional stuff or techniques are used while storing a tree in an array then one traversal can facilitate like also storing null values of a node in array.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “AA Tree”.
1. AA Trees are implemented using?
a) Colors
b) Levels
c) Node size
d) Heaps
Explanation: AA Trees are implemented using levels instead of colors to overcome the disadvantages of Red-Black trees.
2. Which of the following is the correct definition for a horizontal link?
a) connection between node and a child of equal levels
b) connection between two nodes
c) connection between two child nodes
d) connection between root node and leaf node
Explanation: A horizontal link is a connection between a node and a child of equal levels.
3. How will you remove a left horizontal link in an AA-tree?
a) by performing right rotation
b) by performing left rotation
c) by deleting both the elements
d) by inserting a new element
Explanation: A left horizontal link is removed by right rotation. A right horizontal link is removed by left rotation.
4. What are the two different operations done in an AA-Tree?
a) shift and color
b) skew and split
c) zig and zag
d) enqueue and dequeue
Explanation: A skew removes a left horizontal link by right rotation and a split removes a right horizontal link by left rotation.
5. In an AA-tree, we process split first, followed by a skew.
a) True
b) False
Explanation: In an AA-tree, skew is processed first followed by a split.
6. How many different shapes does maintenance of AA-Tree need to consider?
a) 7
b) 5
c) 2
d) 3
Explanation: An AA-Tree needs to consider only two shapes unlike a red-black tree which needs to consider seven shapes of transformation.
7. What is the prime condition of AA-tree which makes it simpler than a red-black tree?
a) Only right children can be red
b) Only left children can be red
c) Right children should strictly be black
d) There should be no left children
Explanation: The prime condition of AA-Tree is that only the right children can be red to eliminate possible restructuring cases.
8. Which of the following trees is similar to that of an AA-Tree?
a) Splay Tree
b) B+ Tree
c) AVL Tree
d) Red-Black Tree
Explanation: AA- Tree is a small variation of Red-Black tree. AA-Trees overcome the complexity faced in performing insertion and deletion in Red-Black Trees.
9. What is the worst case analysis of an AA-Tree?
a) O(N)
b) O(log N)
c) O( N log N)
d) O(N2)
Explanation: The worst case analysis of an AA-Tree is mathematically found to be O(log N).
10. AA-Trees makes more rotations than a red-black tree.
a) True
b) False
Explanation: AA- trees make more rotations than a red-black tree since only two shapes are considered for an AA-Tree whereas seven shapes are considered in Red-Black trees.
11. Who is the inventor of AA-Tree?
a) Arne Anderson
b) Daniel Sleator
c) Rudolf Bayer
d) Jon Louis Bentley
Explanation: AA-tree is invented by Arne Anderson. Daniel Sleator invented Splay Tree. Rudolf Bayer invented a Red-Black tree. Jon Louis Bentley invented K-d tree.
Explanation: The level of a left node should be strictly less than that of its parent. The level of a right node is less than or equal to that of its parent.
13. Of the following rules that are followed by an AA-tree, which of the following is incorrect?
1- Only right children can be red
2- Procedures are coded recursively
3- Instead of storing colors, the level of a node is stored
4- There should not be any left children
a) 1
b) 2
c) 3
d) 4
Explanation: In an AA-Tree, both left and right children can be present. The only condition is that only right children can be red.
14. 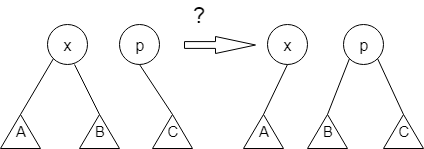
In the given figure, find ‘?’.
a) left rotation
b) right rotation
c) insertion
d) deletion
Explanation: B is initially the right child of X. It is then rotated right side and now, B is the left child of P.
15. Comparing the speed of execution of Red-Black trees and AA-trees, which one has the faster search time?
a) AA-tree
b) Red-Black tree
c) Both have an equal search time
d) It depends
Explanation: Since an AA-tree tends to be flatter, AA-tree has a faster search time than a Red-Black tree.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “B-Tree”.
1. Which of the following is the most widely used external memory data structure?
a) AVL tree
b) B-tree
c) Red-black tree
d) Both AVL tree and Red-black tree
Explanation: In external memory, the data is transferred in form of blocks. These blocks have data valued and pointers. And B-tree can hold both the data values and pointers. So B-tree is used as an external memory data structure.
2. B-tree of order n is a order-n multiway tree in which each non-root node contains __________
a) at most (n – 1)/2 keys
b) exact (n – 1)/2 keys
c) at least 2n keys
d) at least (n – 1)/2 keys
Explanation: A non-root node in a B-tree of order n contains at least (n – 1)/2 keys. And contains a maximum of (n – 1) keys and n sons.
3. A B-tree of order 4 and of height 3 will have a maximum of _______ keys.
a) 255
b) 63
c) 127
d) 188
Explanation: A B-tree of order m of height h will have the maximum number of keys when all nodes are completely filled. So, the B-tree will have n = (mh+1 – 1) keys in this situation. So, required number of maximum keys = 43+1 – 1 = 256 – 1 = 255.
4. Five node splitting operations occurred when an entry is inserted into a B-tree. Then how many nodes are written?
a) 14
b) 7
c) 11
d) 5
Explanation: If s splits occur in a B-tree, 2s + 1 nodes are written (2 halves of each split and the parent of the last node split). So, if 5 splits occurred, then 2 * 5 + 1 , i.e. 11 nodes are written.
5. B-tree and AVL tree have the same worst case time complexity for insertion and deletion.
a) True
b) False
Explanation: Both the B-tree and the AVL tree have O(log n) as worst case time complexity for insertion and deletion.
6. 2-3-4 trees are B-trees of order 4. They are an isometric of _____ trees.
a) AVL
b) AA
c) 2-3
d) Red-Black
Explanation: 2-3-4 trees are isometric of Red-Black trees. It means that, for every 2-3-4 tree, there exists a Red-Black tree with data elements in the same order.
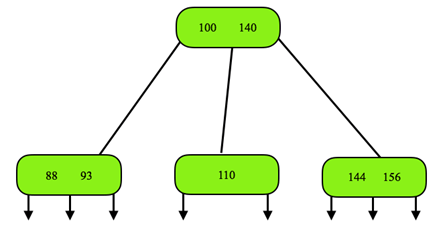
7. Figure shown below is B-tree of order 5. What is the result of deleting 130 from the tree?
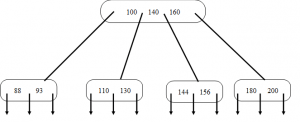
a)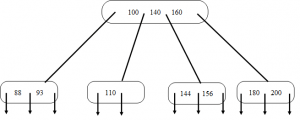
b)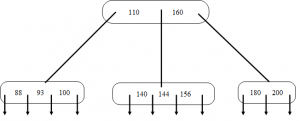
c) 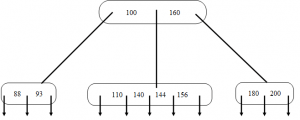
d)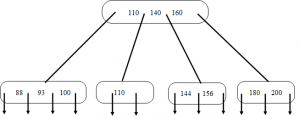
Explanation: Each non-root in a B-tree of order 5 must contain at least 2 keys. Here, when the key 130 is deleted the node gets underflowed i.e. number of keys in the node drops below 2. So we combine the node with key 110 with it’s brother node having keys 144 and 156. And this combined node will also contain the separator key from parent i.e. key 140, leaving the root with two keys 110 and 160.
8. What is the best case height of a B-tree of order n and which has k keys?
a) logn (k+1) – 1
b) nk
c) logk (n+1) – 1
d) klogn
Explanation: B-tree of order n and with height k has best case height h, where h = logn (k+1) – 1. The best case occurs when all the nodes are completely filled with keys.
9. Compression techniques can be used on the keys to reduce both space and time requirements in a B-tree.
a) True
b) False
Explanation: The front compression and the rear compression are techniques used to reduce space and time requirements in B-tree. The compression enables to retain more keys in a node so that the number of nodes needed can be reduced.
10. Which of the following is true?
a) larger the order of B-tree, less frequently the split occurs
b) larger the order of B-tree, more frequently the split occurs
c) smaller the order of B-tree, more frequently the split occurs
d) smaller the order of B-tree, less frequently the split occurs
Explanation: The average probability of the split is 1/(⌈m / 2⌉ – 1), where m is the order of B-tree. So, if m larger, the probability of split will be less.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “2-3 Tree”.
1. 2-3 tree is a specific form of _________
a) B – tree
b) B+ – tree
c) AVL tree
d) Heap
Explanation: The 2-3 trees is a balanced tree. It is a specific form the B – tree. It is B – tree of order 3, where every node can have two child subtrees and one key or 3 child subtrees and two keys.
2. Which of the following is the 2-3 tree?
a)
b)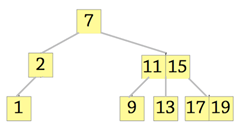
c)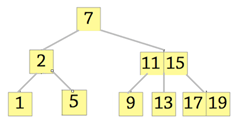
d)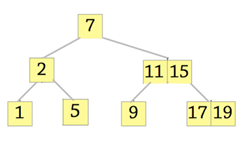
Explanation: Tree should have two subtrees at node2, but it should not have three elements. The node with elements 11 and 15 should have three child subtrees.
3. The height of 2-3 tree with n elements is ______
a) between (n/2) and (n/3)
b) (n/6)
c) between (n) and log2(n + 1)
d) between log3(n + 1) and log2(n + 1)
Explanation: The number of elements in a 2-3 tree with height h is between 2h – 1 and 3h – 1. Therefore, the 2-3 tree with n elements will have the height between log3(n + 1) and log2(n + 1).
4. Which of the following the BST is isometric with the 2-3 tree?
a) Splay tree
b) AA tree
c) Heap
d) Red – Black tree
Explanation: AA tree is isometric of the 2-3 trees. In an AA tree, we store each node a level, which is the height of the corresponding 2-3 tree node. So, we can convert a 2-3 tree to an AA tree.
5. The figure shown below is a 2-3 tree. What is the result of deleting 110 from the tree?
a)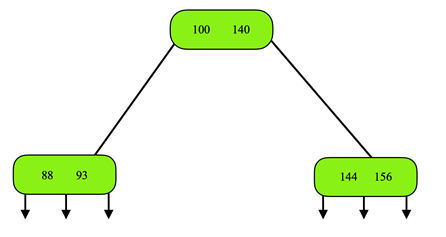
b)
c)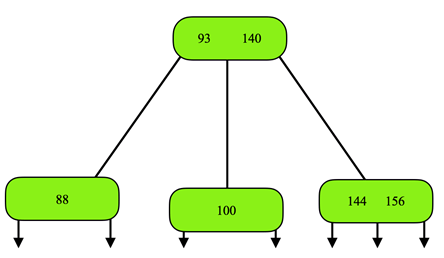
d)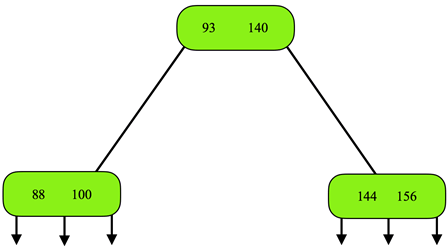
Explanation: When 110 is deleted the respective node becomes empty, so the 2-3 tree properties get violated. Hence, the element from its sibling node, 93 is moved to the root and root node element 100 is fed to the empty node. So, the resultant 2-3 tree will be,

6. Which of the following data structure can provide efficient searching of the elements?
a) unordered lists
b) binary search tree
c) treap
d) 2-3 tree
Explanation: The average case time for lookup in a binary search tree, treap and 2-3 tree is O(log n) and in unordered lists it is O(n). But in the worst case, only the 2-3 trees perform lookup efficiently as it takes O(log n), while others take O(n).
7. LLRB maintains 1-1 correspondence with 2–3 trees.
a) True
b) False
Explanation: LLRB (Left Leaning Red Black tree)is the data structure which is used to implement the 2-3 tree with very basic code. The LLRB is like the 2-3 tree where each node has one key and two links. In LLRB the 3-node is implemented as two 2-nodes connected by the red link that leans left. Thus, LLRB maintains 1-1 correspondence with 2–3 tree.
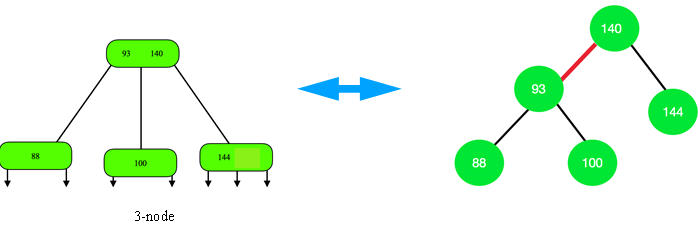
8. Which of the following is not true about the 2-3 tree?
a) all leaves are at the same level
b) it is perfectly balanced
c) postorder traversal yields elements in sorted order
d) it is B-tree of order 3
Explanation: In a 2-3 tree, leaves are at the same level. And 2-3 trees are perfectly balanced as every path from root node to the null link is of equal length. In 2-3 tree in-order traversal yields elements in sorted order.
9. AVL trees provide better insertion the 2-3 trees.
a) True
b) False
Explanation: Insertion in AVL tree and 2-3 tree requires searching for proper position for insertion and transformations for balancing the tree. In both, the trees searching takes O(log n) time, but rebalancing in AVL tree takes O(log n), while the 2-3 tree takes O(1). So, 2-3 tree provides better insertions.
10. Which of the following is false?
a) 2-3 tree requires less storage than the BST
b) lookup in 2-3 tree is more efficient than in BST
c) 2-3 tree is shallower than BST
d) 2-3 tree is a balanced tree
Explanation: Search is more efficient in the 2-3 tree than in BST. 2-3 tree is a balanced tree and performs efficient insertion and deletion and it is shallower than BST. But, 2-3 tree requires more storage than the BST.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Ternary Tree – 1”.
1. How many child nodes does each node of Ternary Tree contain?
a) 4
b) 6
c) 5
d) 3
Explanation: Each node of Ternary tree contains at most 3 nodes. So Ternary tree can have 1, 2 or 3 child nodes but not more than that.
2. Which of the following is the name of the node having child nodes?
a) Brother
b) Sister
c) Mother
d) Parent
Explanation: Parent node is the node having child nodes and child nodes may contain references to their parents. Parent node is a node connected by a directed edge to its child.
3. What is the depth of the root node of the ternary tree?
a) 2
b) 1
c) 0
d) 3
Explanation: Depth is defined as the length of the path from root to the node. So the depth of root node in ternary tree is 0.
4. What is the Height of the root node of ternary tree?
a) 1
b) 2
c) 3
d) 0
Explanation: Height of ternary tree is defined as the length of path from root to deepest node in tree. Therefore, height off root node in ternary tree is 0.
5. Which node is the root node of the following ternary tree?
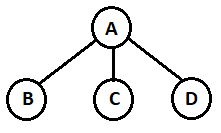
a) A
b) B
c) C
d) D
Explanation: Node A is called the root node of the above ternary tree while the Node B, Node C, Node D are called Leaf node.
6. Which node is the Leaf node in the following ternary tree?
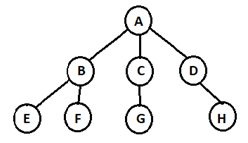
a) A
b) B
c) D
d) G
Explanation: Leaf node is any node that does not contain any children. Since Node G is the node without any children, So G is called Leaf Node. While Node A is root node and Node B, Node C, Node D is parent node of their children.
7. Which node is the parent node of Node 6?
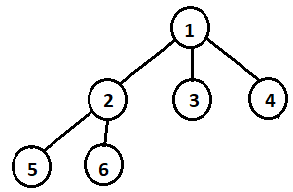
a) 1
b) 5
c) 2
d) 3
Explanation: Since Node 2 has two children Node 5 and Node 6, So Node 2 is the parent node of Node 6. While Node 1 is root node and Node 3 and Node 5 are Leaf node.
8. Is parent node of Node 3 and root node of the given ternary tree same?

a) True
b) False
Explanation: Since Root node of the ternary tree is Node 1 and also Node 1 has three children that is Node 2, Node 3, Node 4. So parent node of Node 3 and the root node of the ternary tree are same.
9. Which node is the child node of Node D in the following ternary tree?

a) A
b) C
c) G
d) H
Explanation: The Child node is the node that has a directed path from its parent node. Since Node D has a direct path to Node H, So Node H is the Child node.
10. Which node is the child node of the Node D in the following ternary tree?

a) A
b) C
c) B
d) No child node
Explanation: Since Node D is the Leaf node of the above ternary tree and leaf node has no child node. So there is no child node for Node D in the above ternary tree.
11. What is the depth of Node G in the given ternary tree?

a) 0
b) 1
c) 2
d) 3
Explanation: Depth of the node is the length of the path from root to the node. Here, length of path from root to Node G is 2. So depth of Node G is 2.
Explanation: Height of the tree is defined as the length of the path from root node to the deepest node of the tree. Here deepest nodes are 5,6,7 which are at length 2. So the height of the ternary tree is 2.
13. Which nodes are the siblings of Node B of given ternary tree?

a) E
b) C
c) F
d) Both E and F
Explanation: Siblings are the nodes that share same parent. Since both the Node E and Node F have same parent Node B, So the sibling of Node B is Node E and Node F.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Disjoint-Set Data Structure”.
1. How many properties will an equivalent relationship satisfy?
a) 1
b) 2
c) 3
d) 4
Explanation: An equivalent relationship will satisfy three properties – reflexive, symmetric and transitive.
2. A relation R on a set S, defined as x R y if and only if y R x. This is an example of?
a) reflexive relation
b) symmetric relation
c) transitive relation
d) invalid relation
Explanation: A symmetric property in an equivalence relation is defined as x R y if and only y R x.
3. Electrical connectivity is an example of equivalence relation.
a) true
b) false
Explanation: Electrical connectivity is reflexive, symmetric and also transitive. Hence, electrical connectivity is an equivalence relation.
4. What is the worst case efficiency for a path compression algorithm?
a) O(N)
b) O(log N)
c) O(N log N)
d) O(M log N)
Explanation: The worst case efficiency for a path compression algorithm is mathematically found to be O(M log N).
5. Path Compression algorithm performs in which of the following operations?
a) Create operation
b) Insert operation
c) Find operation
d) Delete operation
Explanation: Path compression algorithm is performed during find operation and is independent of the strategy used to perform unions.
6. What is the definition for Ackermann’s function?
a) A(1,i) = i+1 for i>=1
b) A(i,j) = i+j for i>=j
c) A(i,j) = i+j for i = j
d) A(1,i) = i+1 for i<1
Explanation: The Ackermann’s function is defined as A(1,i) = i+1 for i>=1. This form in text grows faster and the inverse is slower.
7. ___________ is one of the earliest forms of a self-adjustment strategy used in splay trees, skew heaps.
a) Union by rank
b) Equivalence function
c) Dynamic function
d) Path compression
Explanation: Path compression is one of the earliest forms of self-adjustment used in extremely important strategies using theoretical explanations.
8. What is the depth of any tree if the union operation is performed by height?
a) O(N)
b) O(log N)
c) O(N log N)
d) O(M log N)
Explanation: If the Unions are performed by height, the depth of any tree is calculated to be O(log N).
9. When executing a sequence of Unions, a node of rank r must have at least 2r descendants.
a) true
b) false
Explanation: By the induction hypothesis, each tree has at least 2r – 1 descendants, giving a total of 2r and establishing the lemma.
10. What is the value for the number of nodes of rank r?
a) N
b) N/2
c) N/2r
d) Nr
Explanation: Each node of a rank r is the root of a subtree of at least 2r. Therefore, there are at most N/2r disjoint subtrees.
11. What is the worst-case running time of unions done by size and path compression?
a) O(N)
b) O(logN)
c) O(N logN)
d) O(M logN)
Explanation: The worst case running time of a union operation done by size and path compression is mathematically found to be O(M logN).
Explanation: One of the lemmas state that, in the Union/Find algorithm, the ranks of the nodes on a path will increase monotonically from leaf to root.
13. How many strategies are followed to solve a dynamic equivalence problem?
a) 1
b) 2
c) 3
d) 4
Explanation: There are two strategies involved to solve a dynamic equivalence problem- executing find instruction in worst-case time and executing union instruction in worst-case time.
14. What is the total time spent for N-1 merges in a dynamic equivalence problem?
a) O(N)
b) O(log N)
c) O(N log N)
d) O(M log N)
Explanation: The total time spent for N-1 merges in a dynamic equivalence problem is mathematically found to be O(N log N).
15. What is the condition for an equivalence relation if two cities are related within a country?
a) the two cities should have a one-way connection
b) the two cities should have a two-way connection
c) the two cities should be in different countries
d) no equivalence relation will exist between two cities
Explanation: If the two towns are in the same country and have a two-way road connection between them, it satisfies equivalence property.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Heap”.
1. In a max-heap, element with the greatest key is always in the which node?
a) Leaf node
b) First node of left sub tree
c) root node
d) First node of right sub tree
Explanation: This is one of the property of max-heap that root node must have key greater than its children.
2. Heap exhibits the property of a binary tree?
a) True
b) False
Explanation: Yes, because the leaf nodes are present at height h or h-1, which is a property of complete binary tree.
3. What is the complexity of adding an element to the heap.
a) O(log n)
b) O(h)
c) O(log n) & O(h)
d) O(n)
Explanation: The total possible operation in re locating the new location to a new element will be equal to height of the heap.
4. The worst case complexity of deleting any arbitrary node value element from heap is __________
a) O(logn)
b) O(n)
c) O(nlogn)
d) O(n2)
Explanation: The total possible operation in deleting the existing node and re locating new position to all its connected nodes will be equal to height of the heap.
5. Heap can be used as ________________
a) Priority queue
b) Stack
c) A decreasing order array
d) Normal Array
Explanation: The property of heap that the value of root must be either greater or less than both of its children makes it work like a priority queue.
6.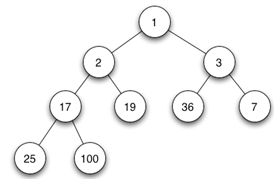
If we implement heap as min-heap, deleting root node (value 1)from the
heap. What would be the value of root node after second iteration if
leaf node (value 100) is chosen to replace the root at start.
a) 2
b) 100
c) 17
d) 3
Explanation: As the root is deleted and node with value 100 is used as replaced one. There is a violation of property that root node must have value less than its children. So there will be shuffling of node with value 100 with node of value 2. And thus 2 becomes root. And it will remain to be at root after all the possible operations. So the value at root will be 2.
7.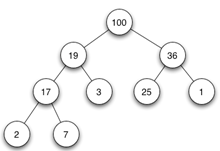
If we implement heap as maximum heap , adding a new node of value 15 to
the left most node of right subtree . What value will be at leaf nodes
of the right subtree of the heap.
a) 15 and 1
b) 25 and 1
c) 3 and 1
d) 2 and 3
Explanation: As 15 is less than 25 so there would be no violation and the node will remain at that position. So leaf nodes with value 15 and 1 will be at the position in right sub tree.
8. An array consists of n elements. We want to create a heap using
the elements. The time complexity of building a heap will be in order of
a) O(n*n*logn)
b) O(n*logn)
c) O(n*n)
d) O(n *logn *logn)
Explanation: The total time taken will be N times the complexity of adding a single element to the heap. And adding a single element takes logN time, so That is equal to N*logN.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Ternary Heap – 2”.
1. What is the time complexity for inserting a new item in a ternary heap of n elements?
a) O (log n/ log 3)
b) O (n!)
c) O (n)
d) O (1)
Explanation: In order to insert a new item in a ternary heap data structure having n elements, the heap has great efficiency for inserting them. So the time complexity for worst case is found to be O (log n/ log 3).
2. Is decrease priority operation performed more quickly in a ternary heap with respect to the binary heap.
a) True
b) False
Explanation: Ternary heap is a type of data structure in the field of computer science. It is a part of the Heap data structure family. Due to the swapping process, the decrease priority operation performs more quickly in a ternary heap.
3. What is the time complexity for decreasing priority of key in a minimum ternary heap of n elements?
a) O (log n/ log 3)
b) O (n!)
c) O (n)
d) O (1)
Explanation: In order to decrease the priority of an item in a ternary heap data structure having n elements, the heap has great efficiency for decreasing them. So the time complexity for worst case is found to be O (log n/ log 3). This is due to the upwards swapping process.
4. What is the time complexity for increasing priority of key in a maximum ternary heap of n elements?
a) O (log n/ log 3)
b) O (n!)
c) O (n)
d) O (1)
Explanation: In order to increase the priority of an item in a ternary heap data structure having n elements, it performs upwards swapping. So the time complexity for worst case is found to be O (log n/ log 3).
5. What is the time complexity for deleting root key in a ternary heap of n elements?
a) O (log n/ log 3)
b) O (3log n/ log 3)
c) O (n)
d) O (1)
Explanation: In order to delete a root key in a ternary heap data structure having n elements, it performs downward swapping. So the time complexity for worst case is found to be O (3log n/ log 3).
6. What is the time complexity for increasing priority of key in a minimum ternary heap of n elements?
a) O (log n/ log 3)
b) O (3log n/ log 3)
c) O (n)
d) O (1)
Explanation: In order to the increasing the priority of key in a minimum ternary heap data structure having n elements, it performs downward swapping. So the time complexity for worst case is found to be O (3log n/ log 3).
7. What is the time complexity for decreasing priority of key in a maximum ternary heap of n elements?
a) O (log n/ log 3)
b) O (3log n/ log 3)
c) O (n)
d) O (1)
Explanation: In order to decrease the priority of key in a maximum ternary heap data structure having n elements, it performs downward swapping. So the time complexity for worst case is found to be O (3log n/ log 3).
8. Do ternary heap have better memory cache behavior than binary heap.
a) True
b) False
Explanation: Ternary heap is a type of data structure in the field of computer science. It is a part of the Heap data structure family. Due to the swapping process, they have better memory cache behavior.
9. What is the time complexity for creating a ternary heap using swapping?
a) O (log n/ log 3)
b) O (n!)
c) O (n)
d) O (1)
Explanation: Ternary Heap can be formed by two swapping operations. Therefore, the time complexity for creating a ternary heap using two swapping operation is found to be O (n).
10. Which of the following is the application of minimum ternary heap?
a) Prim’s Algorithm
b) Euclid’s Algorithm
c) Eight Queen Puzzle
d) Tree
Explanation: When working on the graph in the computer science field, the Prim’s Algorithm for spanning trees uses a minimum ternary heap as there are delete operation equal to a number of edges and decrease priority operation equal to the number of vertices associated with the graph.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Trie”.
1. Trie is also known as _________
a) Digital Tree
b) Treap
c) Binomial Tree
d) 2-3 Tree
Explanation: Trie is a very useful data structure which is based on the prefix of a string. Trie is used to represent the “Retrieval” of data and thus the name Trie. And it is also known as a digital tree.
2. What traversal over trie gives the lexicographical sorting of the set of the strings?
a) postorder
b) preorders
c) inorder
d) level order
Explanation: In trie, we store the strings in such a way that there is one node for every common prefix. Therefore the inorder traversal over trie gives the lexicographically sorted set of strings.
3. Which of the following is the efficient data structure for searching words in dictionaries?
a) BST
b) Linked List
c) Balancded BST
d) Trie
Explanation: In a BST, as well as in a balanced BST searching takes time in order of mlogn, where m is the maximum string length and n is the number of strings in tree. But searching in trie will take O(m) time to search the key.
4. Which of the following special type of trie is used for fast searching of the full texts?
a) Ctrie
b) Hash tree
c) Suffix tree
d) T tree
Explanation: Suffix tree, a special type of trie, contains all the suffixes of the given text at the key and their position in the text as their values. So, suffix trees are used for fast searching of the full texts.
5. Following code snippet is the function to insert a string in a trie. Find the missing line.
private insertString str
TrieNode node root
i i length i
index key.i
node.index
node.index new TrieNode
________________________
node.
a) node = node.children[index];
b) node = node.children[str.charAt(i + 1)];
c) node = node.children[index++];
d) node = node.children[index++];
Explanation: In the insert() method we search if the string is present or not. If the string is not present, then we insert the string into the trie. If it is present as the prefix, we mark the leaf node. So, correct option is node = node.children[index];.
6. Which of the following is not true?
a) Trie requires less storage space than hashing
b) Trie allows listing of all the words with same prefix
c) Tries are collision free
d) Trie is also known as prefix tree
Explanation: Both the hashing and the trie provides searching in the linear time. But trie requires extra space for storage and it is collision free. And trie allows finding all the strings with same prefix, so it is also called prefix tree.
7. A program to search a contact from phone directory can be implemented efficiently using ______
a) a BST
b) a trie
c) a balanced BST
d) a binary tree
Explanation: Dictionaries, phone directories can be implemented efficiently using the trie. Because it trie provides the efficient linear time searching over the entries.
8. What can be the maximum depth of the trie with n strings and m as the maximum sting the length?
a) log2n
b) log2m
c) n
d) m
Explanation: In the trie, the strings are stored efficiently based on the common prefixes. And trie has maximum fan-out 26 if english alphabets are considered. Owing to this, the maximum depth is equal to the maximum string length.
9. Which of the following is true about the trie?
a) root is letter a
b) path from root to the leat yields the string
c) children of nodes are randomly ordered
d) each node stores the associated keys
Explanation: A trie is an ordered tree where (i) the root represents an empty string(“”) (ii) each node other than root is labeled with a character (iii) the children of a nodes are lexicographically ordered (iv) the paths from the leaves to the root yields the strings.
10. Auto complete and spell checkers can be implemented efficiently using the trie.
a) True
b) False
Explanation: Trie provides fast searching and storing of the words. And tries stores words in lexicographical order so, trie is the efficient data structure for implementation of spell checkers and auto complete.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Suffix Tree – 2”.
1. What is a time complexity for x pattern occurrence of length n?
a) O (log n!)
b) Ɵ (n!)
c) O (n2)
d) Ɵ (n + x)
Explanation: Suffix tree is also known as PAT tree or position tree. It allows fast string operation. To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for x pattern occurrence of length n is Ɵ (n + x).
2. What is a time complexity for finding the longest substring that
is common in string S1 and S2 (n1 and n2 are the string lengths of
strings s1, s2 respectively)?
a) O (log n!)
b) Ɵ (n!)
c) O (n2+ n1)
d) Ɵ (n1 + n2)
Explanation: Suffix Tree allows fast string operation. To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for finding the longest substring that is common in string S1 and S2 is Ɵ (n1 + n2).
3. What is a time complexity for finding the longest substring that is repeated in a string?
a) O (log n!)
b) Ɵ (n!)
c) O (n2+ n1)
d) Ɵ (n)
Explanation: Suffix Tree allows fast string operation. To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for finding the longest substring that is repeated in a string is Ɵ (n).
4. What is a time complexity for finding frequently occurring of a substring of minimum length in a string?
a) Ɵ (n)
b) Ɵ (n!)
c) O (n2+ n1)
d) O (log n!)
Explanation: Suffix Tree allows fast string operation. To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for finding frequently occurring of a substring of minimum length in a string is Ɵ (n).
5. What is a time complexity for finding the longest prefix that is common between suffix in a string?
a) Ɵ (n)
b) Ɵ (n!)
c) Ɵ (1)
d) O (log n!)
Explanation: Suffix Tree allows fast string operation. To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for finding the longest prefix that is common between suffix in a string is Ɵ (1).
6. What is a time complexity for finding all the maximal palindrome in a string?
a) Ɵ (n)
b) Ɵ (n!)
c) Ɵ (1)
d) O (log n!)
Explanation: Palindrome is a string that is the same when reading forward as well as backward. To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for finding all the maximal palindrome in a string is Ɵ (n).
7. What is a time complexity for finding all the tandem repeats?
a) Ɵ (n)
b) Ɵ (n!)
c) Ɵ (1)
d) O (n log n + z)
Explanation: Tandem Repeats are formed in DNA when the nucleotides pattern repeats more than once. To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for finding all the tandem repeats in a string is O (n log n + z).
8. What is a time complexity for finding the longest palindromic substring in a string by using the generalized suffix tree?
a) Linear Time
b) Exponential Time
c) Logarithmic Time
d) Cubic Time
Explanation: Palindrome is a string that is same when reading forward as well as backward. The time complexity for finding the longest palindromic substring in a string by using generalized suffix tree is linear time.
9. Which of the following algorithm of data compression uses a suffix tree?
a) Weiner’s algorithm
b) Farach’s algorithm
c) Lempel – Ziv – Welch’s algorithm
d) Alexander Morse’s algorithm
Explanation: The concept of Suffix Tree was introduced by Weiner in 1973. Ukkonen provided the first online contribution of the Suffix tree. Farach gave the first suffix tree contribution for all alphabets in 1997. Lempel – Ziv – Welch’s algorithm of data compression uses a suffix tree.
10. Which of the following data clustering algorithm uses suffix tree in search engines?
a) Weiner’s algorithm
b) Farach’s algorithm
c) Lempel – Ziv – Welch’s algorithm
d) Suffix Tree Clustering
Explanation: The concept of Suffix Tree was introduced by Weiner in 1973. Ukkonen provided the first online contribution of Suffix. Farach gave the first suffix tree contribution for all alphabets in 1997. Suffix Tree Clustering is a data clustering algorithm that uses suffix tree in search engines.
11. What is a time complexity for finding the total length of all string on all edges of a tree?
a) Ɵ (n)
b) Ɵ (n!)
c) Ɵ (1)
d) O (n2)
Explanation: To check if a substring is present in a string of a length of n, the time complexity for such operation is found to be O (n). The time complexity for finding the total length of all string on all edges of a tree is O (n2).
Explanation: It is a compressed search tree or prefix tree in which keys contain the suffix of text values as the text position. So, the suffix tree can be used in string problems occurring in a text editor. The time taken to solve the problem is linear to the length of the string.
13. Can suffix tree be used in bioinformatics problems and solutions.
a) True
b) False
Explanation: It is a compressed search tree or prefix tree in which keys contain the suffix of text values as the text position. So, a suffix tree is used in bioinformatics problems and solutions like pattern searching in DNA and protein sequences.
14. For what size of nodes, the worst case of usage of space in suffix tree seen?
a) n Nodes
b) 2n Nodes
c) 2n nodes
d) n! nodes
Explanation: In computer science, the worst case of usage of space in a suffix tree is found to be for a Fibonacci word for a full 2n nodes. The time complexity for usage of space is found to be O (n).
15. What is a time complexity for inserting an alphabet in the tree using hash maps?
a) O (log n!)
b) O (n!)
c) O (n2)
d) O (1)
Explanation: Suffix tree is also known as PAT tree or position tree. It allows fast string operation. Total time taken for construction of suffix tree is linear to the length of the tree. The time complexity for inserting an alphabet in the tree using hash maps is constant, O (1).
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Hash Tables”.
1. What is a hash table?
a) A structure that maps values to keys
b) A structure that maps keys to values
c) A structure used for storage
d) A structure used to implement stack and queue
Explanation: A hash table is used to implement associative arrays which has a key-value pair, so the has table maps keys to values.
2. If several elements are competing for the same bucket in the hash table, what is it called?
a) Diffusion
b) Replication
c) Collision
d) Duplication
Explanation: In a hash table, if sevaral elements are computing for the same bucket then there will be a clash among elements. This condition is called Collision. The Collision is reduced by adding elements to a linked list and head address of linked list is placed in hash table.
3. What is direct addressing?
a) Distinct array position for every possible key
b) Fewer array positions than keys
c) Fewer keys than array positions
d) Same array position for all keys
Explanation: Direct addressing is possible only when we can afford to allocate an array that has one position for every possible key.
4. What is the search complexity in direct addressing?
a) O(n)
b) O(logn)
c) O(nlogn)
d) O(1)
Explanation: Since every key has a unique array position, searching takes a constant time.
5. What is a hash function?
a) A function has allocated memory to keys
b) A function that computes the location of the key in the array
c) A function that creates an array
d) A function that computes the location of the values in the array
Explanation: In a hash table, there are fewer array positions than the keys, so the position of the key in the array has to be computed, this is done using the hash function.
6. Which of the following is not a technique to avoid a collision?
a) Make the hash function appear random
b) Use the chaining method
c) Use uniform hashing
d) Increasing hash table size
Explanation: On increasing hash table size, space complexity will increase as we need to reallocate the memory size of hash table for every collision. It is not the best technique to avoid a collision. We can avoid collision by making hash function random, chaining method and uniform hashing.
7. What is the load factor?
a) Average array size
b) Average key size
c) Average chain length
d) Average hash table length
Explanation: In simple chaining, load factor is the average number of elements stored in a chain, and is given by the ratio of number of elements stored to the number of slots in the array.
8. What is simple uniform hashing?
a) Every element has equal probability of hashing into any of the slots
b) A weighted probabilistic method is used to hash elements into the slots
c) Elements has Random probability of hashing into array slots
d) Elements are hashed based on priority
Explanation: In simple uniform hashing, any given element is equally likely to hash into any of the slots available in the array.
9. In simple uniform hashing, what is the search complexity?
a) O(n)
b) O(logn)
c) O(nlogn)
d) O(1)
Explanation: There are two cases, once when the search is successful and when it is unsuccessful, but in both the cases, the complexity is O(1+alpha) where 1 is to compute the hash function and alpha is the load factor.
10. In simple chaining, what data structure is appropriate?
a) Singly linked list
b) Doubly linked list
c) Circular linked list
d) Binary trees
Explanation: Deletion becomes easier with doubly linked list, hence it is appropriate.
This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Hash Tables with Quadratic Probing”.
1. Which of the following schemes does quadratic probing come under?
a) rehashing
b) extended hashing
c) separate chaining
d) open addressing
Explanation: Quadratic probing comes under open addressing scheme to resolve collisions in hash tables.
2. Quadratic probing overcomes primary collision.
a) True
b) False
Explanation: Quadratic probing can overcome primary collision that occurs in linear probing but a secondary collision occurs in quadratic probing.
3. What kind of deletion is implemented by hashing using open addressing?
a) active deletion
b) standard deletion
c) lazy deletion
d) no deletion
Explanation: Standard deletion cannot be performed in an open addressing hash table, because the cells might have caused collision. Hence, the hash tables implement lazy deletion.
4. In quadratic probing, if the table size is prime, a new element cannot be inserted if the table is half full.
a) True
b) False
Explanation: In quadratic probing, if the table size is prime, we can insert a new element even though table is exactly half filled. We can’t insert element if table size is more than half filled.
5. Which of the following is the correct function definition for quadratic probing?
a) F(i)=i2
b) F(i)=i
c) F(i)=i+1
d) F(i)=i2+1
Explanation: The function of quadratic probing is defined as F(i)=i2. The function of linear probing is defined as F(i)=i.
6. How many constraints are to be met to successfully implement quadratic probing?
a) 1
b) 2
c) 3
d) 4
Explanation: 2 requirements are to be met with respect to table size. The table size should be a prime number and the table size should not be more than half full.
7. Which among the following is the best technique to handle collision?
a) Quadratic probing
b) Linear probing
c) Double hashing
d) Separate chaining
Explanation: Quadratic probing handles primary collision occurring in the linear probing method. Although secondary collision occurs in quadratic probing, it can be removed by extra multiplications and divisions.
8. Which of the following techniques offer better cache performance?
a) Quadratic probing
b) Linear probing
c) Double hashing
d) Rehashing
Explanation: Linear probing offers better cache performance than quadratic probing and also it preserves locality of reference.
9. What is the formula used in quadratic probing?
a) Hash key = key mod table size
b) Hash key=(hash(x)+F(i)) mod table size
c) Hash key=(hash(x)+F(i2)) mod table size
d) H(x) = x mod 17
Explanation: Hash key=(hash(x)+F(i2)) mod table size is the formula for quadratic probing. Hash key = (hash(x)+F(i)) mod table size is the formula for linear probing.
10. For the given hash table, in what location will the element 58 be hashed using quadratic probing?
| 0 | 49 |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | 18 |
| 9 | 89 |
a) 1
b) 2
c) 7
d) 6
Explanation: Initially, 58 collides at position 8. Another collision occurs one cell away. Hence, F(i2)=4. Using quadratic probing formula, the location is obtained as 2.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Graph”.
1. Which of the following statements for a simple graph is correct?
a) Every path is a trail
b) Every trail is a path
c) Every trail is a path as well as every path is a trail
d) Path and trail have no relation
Explanation: In a walk if the vertices are distinct it is called a path, whereas if the edges are distinct it is called a trail.
2. In the given graph identify the cut vertices.
a) B and E
b) C and D
c) A and E
d) C and B
Explanation: After removing either B or C, the graph becomes disconnected.
3. For the given graph(G), which of the following statements is true?
a) G is a complete graph
b) G is not a connected graph
c) The vertex connectivity of the graph is 2
d) The edge connectivity of the graph is 1
Explanation: After removing vertices B and C, the graph becomes disconnected.
4. What is the number of edges present in a complete graph having n vertices?
a) (n*(n+1))/2
b) (n*(n-1))/2
c) n
d) Information given is insufficient
Explanation: Number of ways in which every vertex can be connected to each other is nC2.
5. The given Graph is regular.
a) True
b) False
Explanation: In a regular graph, degrees of all the vertices are equal. In the given graph the degree of every vertex is 3.
6. In a simple graph, the number of edges is equal to twice the sum of the degrees of the vertices.
a) True
b) False
Explanation: The sum of the degrees of the vertices is equal to twice the number of edges.
7. A connected planar graph having 6 vertices, 7 edges contains _____________ regions.
a) 15
b) 3
c) 1
d) 11
Explanation: By euler’s formula the relation between vertices(n), edges(q) and regions(r) is given by n-q+r=2.
8. If a simple graph G, contains n vertices and m edges, the number of edges in the Graph G'(Complement of G) is ___________
a) (n*n-n-2*m)/2
b) (n*n+n+2*m)/2
c) (n*n-n-2*m)/2
d) (n*n-n+2*m)/2
Explanation: The union of G and G’ would be a complete graph so, the number of edges in G’= number of edges in the complete form of G(nC2)-edges in G(m).
9. Which of the following properties does a simple graph not hold?
a) Must be connected
b) Must be unweighted
c) Must have no loops or multiple edges
d) Must have no multiple edges
Explanation: A simple graph maybe connected or disconnected.
10. What is the maximum number of edges in a bipartite graph having 10 vertices?
a) 24
b) 21
c) 25
d) 16
Explanation: Let one set have n vertices another set would contain 10-n vertices.
Total number of edges would be n*(10-n), differentiating with respect to n, would yield the answer.
11. Which of the following is true?
a) A graph may contain no edges and many vertices
b) A graph may contain many edges and no vertices
c) A graph may contain no edges and no vertices
d) A graph may contain no vertices and many edges
Explanation: A graph must contain at least one vertex.
Explanation: For any connected graph with no cycles the equation holds true.
13. For which of the following combinations of the degrees of vertices would the connected graph be eulerian?
a) 1,2,3
b) 2,3,4
c) 2,4,5
d) 1,3,5
Explanation: A graph is eulerian if either all of its vertices are even or if only two of its vertices are odd.
14. A graph with all vertices having equal degree is known as a __________
a) Multi Graph
b) Regular Graph
c) Simple Graph
d) Complete Graph
Explanation: The given statement is the definition of regular graphs.
15. Which of the following ways can be used to represent a graph?
a) Adjacency List and Adjacency Matrix
b) Incidence Matrix
c) Adjacency List, Adjacency Matrix as well as Incidence Matrix
d) No way to represent
Explanation: Adjacency Matrix, Adjacency List and Incidence Matrix are used to represent a graph.
This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Directed Graph”.
1. Dijkstra’s Algorithm will work for both negative and positive weights?
a) True
b) False
Explanation: Dijkstra’s Algorithm assumes all weights to be non-negative.
2. A graph having an edge from each vertex to every other vertex is called a ___________
a) Tightly Connected
b) Strongly Connected
c) Weakly Connected
d) Loosely Connected
Explanation: This is a part of the nomenclature followed in Graph Theory.
3. What is the number of unlabeled simple directed graph that can be made with 1 or 2 vertices?
a) 2
b) 4
c) 5
d) 9
4. Floyd Warshall Algorithm used to solve the shortest path problem has a time complexity of __________
a) O(V*V)
b) O(V*V*V)
c) O(E*V)
d) O(E*E)
Explanation: The Algorithm uses Dynamic Programming and checks for every possible path.
5. All Graphs have unique representation on paper.
a) True
b) False
Explanation: Same Graph may be drawn in different ways on paper.
6. Assuming value of every weight to be greater than 10, in which of
the following cases the shortest path of a directed weighted graph from 2
vertices u and v will never change?
a) add all values by 10
b) subtract 10 from all the values
c) multiply all values by 10
d) in both the cases of multiplying and adding by 10
Explanation: In case of addition or subtraction the shortest path may change because the number of edges between different paths may be different, while in case of multiplication path wont change.
7. What is the maximum possible number of edges in a directed graph with no self loops having 8 vertices?
a) 28
b) 64
c) 256
d) 56
Explanation: If a graph has V vertices than every vertex can be connected to a possible of V-1 vertices.
8. What would be the DFS traversal of the given Graph?
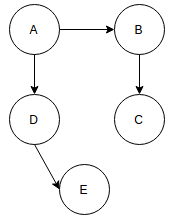
a) ABCED
b) AEDCB
c) EDCBA
d) ADECB
Explanation: In this case two answers are possible including ADEBC.
9. What would be the value of the distance matrix, after the execution of the given code?
graphVV , , INF, ,
INF, , , INF,
INF, INF, , ,
INF, INF, INF,
distanceVV, i, j, k
i i V i
j j V j
distanceij graphij
k k V k
i i V i
j j V j
distanceik distancekj distanceij
distanceij distanceik distancekj
a)
, , INF, ,
INF, , , INF,
INF, INF, , ,
INF, INF, INF,
b)
, , , ,
INF, , , ,
INF, INF, , ,
INF, INF, INF,
, INF, , ,
INF, INF, , ,
INF, INF, , ,
INF, INF, INF,
INF, , , ,
INF, INF, , ,
, INF, INF,
d) None of the mentioned
Explanation: The program computes the shortest sub distances.
10. What is the maximum number of edges present in a simple directed
graph with 7 vertices if there exists no cycles in the graph?
a) 21
b) 7
c) 6
d) 49
Explanation: If the no cycles exists then the difference between the number of vertices and edges is 1.

